[알고리즘] 코딩 테스트 시작을 위한 기초 : 복잡도 분석, C++ 입출력, STL
복잡도란 무엇인가?
계산 복잡도 이론에서 정의하는 복잡도는 크게 시간 복잡도와 공간 복잡도가 있다.
시간 복잡도는 문제를 해결하는데 걸리는 시간과 입력의 함수 관계를 말하고, 공간 복잡도는 문제를 해결하는데 사용되는 메모리 공간과 입력의 함수 관계를 말한다.
시간 복잡도와 공간 복잡도는 반비례 관계에 있다. 다시 말해, 경제학적으로 보면 일종의 파레토 효율적인 상태에서 알고리즘의 수행 시간이 짧아지려면 메모리 공간을 더 많이 쓰면 (메모리 공간을 희생하면) 된다는 것이다.
시간 복잡도
시간 복잡도를 쉽게 말하면, 프로그램 수행시간을 분석하는 것이다. 그래서 반복문에 크게 영향을 받는다. 알고리즘의 시간 복잡도는 주로 빅-오 표기법을 사용하여 나타낸다. 빅-오 표기법에서는 최고차항의 계수와 그보다 낮은 차수의 항을 제외시켜서 표기한다.
빅-오 표기법은 알고리즘이 최악일 때의 경우를 판단한다고 이야기 한다. 예를 들어,
some_list = [1,2,3,4,5] 이와 같은 list를 앞에서부터 탐색하여 숫자 5를 찾아내면 5번만에 찾아낼 것이다. 만약에 5가 맨 앞에 있었으면 제일 처음 찾아낼 것이지만, 빅-오 표기법은 이처럼 최악의 경우를 나타내는 표기법이다.
시간 복잡도에서 주의해야할 점은 시간 복잡도가 실제 실행시간이 아닌 연산수치로 판별하는 개념이라는 것이다. 명령어의 실행시간은 컴퓨터의 하드웨어 또는 프로그래밍 언어에 따라 편차가 존재하기 때문에 명령어의 실행 횟수 등으로 성능을 평가하는 것이다.
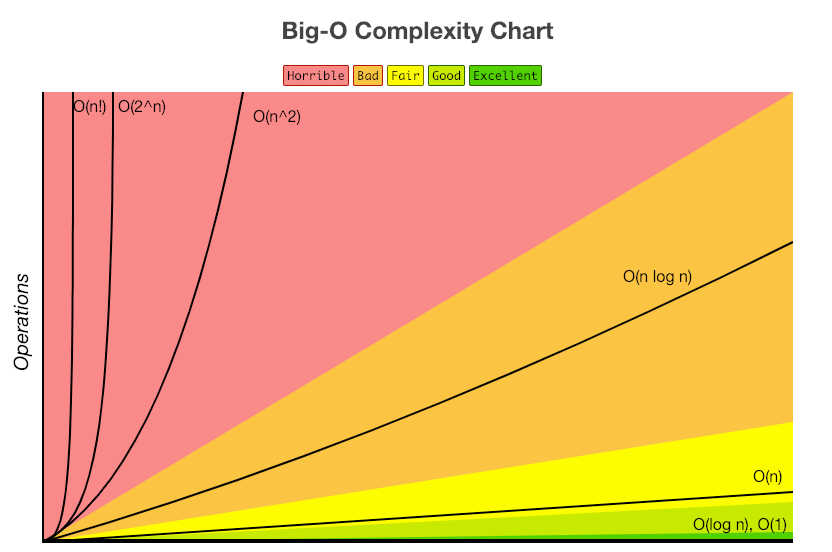
시간 복잡도의 문제해결 단계를 나열 하면 아래와 같다.
O(1) – 상수 시간 : 문제를 해결하는데 오직 한 단계만 처리함.
O(log n) – 로그 시간 : 문제를 해결하는데 필요한 단계들이 연산마다 특정 요인에 의해 줄어듬.
O(n) – 직선적 시간 : 문제를 해결하기 위한 단계의 수와 입력값 n이 1:1 관계를 가짐.
O(n log n) : 문제를 해결하기 위한 단계의 수가 N*(log2N) 번만큼의 수행시간을 가진다. (선형로그형)
O(n^2) – 2차 시간 : 문제를 해결하기 위한 단계의 수는 입력값 n의 제곱.
O(C^n) – 지수 시간 : 문제를 해결하기 위한 단계의 수는 주어진 상수값 C 의 n 제곱.
O(1)
입력에 관계없이 복잡도는 동일하게 유지된다.
void hello_word()
{
std::cout << "hello, world";
}
O(log n)
입력이 증가함에 따라 처리 시간이 선형적으로 증가한다.
void print_each(li)
{
for (auto item : li) std::cout << item;
}
O(n^2)
이중 반복문으로 square 연산이 수행된다.
void print_each_n_times(li)
{
for (auto n : li)
{
for (auto m : li)
{
std::cout << n << m;
}
}
}
공간 복잡도
공간 복잡도를 쉽게 말하면 프로그램의 메모리 사용량을 분석하는 것이다. 간단하게 사용한 배열의 크기 * (해당 자료형의 크기)로 계산하면 된다.
C++ 입출력
C++은 C의 헤더파일을 모두 사용할 수 있고, 추가적으로 C++의 STL 컨테이너들도 사용할 수 있다.
알고리즘 풀이를 하는데 있어서 C++라는 무기를 자유자재로 사용하면 베스트이겠지만, 코딩 테스트만을 위해서 C++의 문법을 샅샅히 공부하는 것은 비효율적이다. 그래서 간단히 C++의 입출력 방법과 자주 사용되는 STL 컨테이너를 살펴보자.
iostream
< iostream > 헤더 파일은 cin, cout 등 기본 입출력 함수 등을 포함하는 기본적인 헤더파일이다.
주로 코딩 테스트를 풀 때 cin을 통해 입력값을 받고 cout을 통해 출력한다. 아래의 코드를 예시로 살펴보자.
#include <iostream>
int main()
{
int n;
std::cin >> n; // cin을 통해 받은 입력을 n에 저장
std::cout << n; << std::endl; // n을 출력
std::cout << "Hello, World!" << std::endl;
return 0;
}
cin은 별도의 입력 타입을 설정해주지 않아도 자동으로 타입을 판단하여 입력받고, cout도 마찬가지이다. 또한 모든 입출력 스트림 클래스는 소유하고 있는 자원(버퍼나 파일 핸들 등)을 해제하는 소멸자를 포함한다.
사실 입출력에 대해 파고들면 양이 매우 방대하다. 기본적인 문제 풀이에서는 입출력에 관해 이정도만 이해하고 있어도 무방하다. 입출력에 대해 깊게 알고 싶다면 A tour of C++ 의 입력과 출력 챕터나 이 블로그 링크를 참고하자.
자주 사용되는 STL
해당 내용은 박트리님 블로그의 내용입니다.
1. vector
동적 배열이다. 아래와 같은 방식으로 사용된다. 임의의 위치에 있는 원소 접근과, 뒤에 원소를 추가하는 연산은 O(1)을 보장한다.
#include <iostream>
#include <vector>
using namespace std;
int main(){
//int 자료형을 저장하는 동적배열
vector<int> vec1;
//double 자료형을 저장하는 동적배열
vector<double> vec2;
//사용자가 정의한 Node 구조체를 저장하는 동적배열
vector<Node> vec3;
//벡터의 초기 크기를 n으로 설정
vector<int> vec4(n);
//벡터의 초기 크기를 n으로 설정하고 1로 초기화
vector<int> vec5(n, 1);
//크기가 n*m인 2차원 벡터를 선언하고 0으로 초기화
vector<vector<int> > vec6(n, vector<int>(m, 0));
//벡터의 맨 뒤에 원소(5) 추가
vec1.push_back(5);
//벡터의 맨 뒤 원소 삭제
vec1.pop_back();
//벡터의 크기 출력
printf("%d\n", vec1.size());
//벡터의 크기를 n으로 재설정
vec1.resize(n);
//벡터의 모든 원소 삭제
vec1.clear();
//벡터의 첫 원소의 주소, 마지막 원소의 다음 주소 리턴
vec1.begin();
vec1.end();
//[a, b) 주소 구간에 해당하는 원소 삭제
vec1.erase(vec1.begin(), vec1.end());//모든 원소 삭제
//vec7은 vec1의 2번째 원소부터 마지막 원소까지 복사하여 생성
vector<int> vec7=vector<int>(vec1.begin()+2, vec1.end());
return 0;
}
2. stack
스택 자료구조이다.
#include <iostream>
#include <stack>
using namespace std;
int main(){
//int자료형을 저장하는 스택 생성
stack<int> st;
//원소(4) 삽입
st.push(4);
//맨 위 원소 팝
st.pop();
//맨 위 원소 값 출력
printf("%d\n", st.top());
//스택이 비어있다면 1 아니면 0
printf("%d\n", st.empty());
//스택에 저장되어 있는 원소의 수 출력
printf("%d\n", st.size());
return 0;
}
3.queue
큐 자료구조이다.
#include <iostream>
#include <queue>
using namespace std;
int main(){
//int자료형을 저장하는 큐 생성
queue<int> q;
//원소(4) 삽입
q.push(4);
//맨 위 원소 팝
q.pop();
//맨 위 원소 값 출력
printf("%d\n", q.front());
//큐가 비어있다면 1 아니면 0
printf("%d\n", q.empty());
//큐에 저장되어 있는 원소의 수 출력
printf("%d\n", q.size());
return 0;
}
4. deque
동적 배열이다. 임의의 위치에 있는 원소의 접근과, 앞과 뒤에 원소를 추가하는 연산은 O(1)을 보장한다.
#include <iostream>
#include <deque>
using namespace std;
int main(){
//int 자료형을 저장하는 동적배열 생성
deque<int> dq;
//배열 맨 앞에 원소(5) 추가
dq.push_front(5);
//배열 맨 뒤에 원소(5) 추가
dq.push_back(5);
//배열 맨 앞의 원소 삭제
dq.pop_front();
//배열 맨 뒤의 원소 삭제
dq.pop_back();
//나머지는 vector와 동일하다.
return 0;
}
5. set
균형 잡힌 이진트리이다. 원소의 삽입과 삭제, 탐색 등의 연산은 O(log n)을 보장한다.
#include <iostream>
#include <set>
using namespace std;
int main(){
//int 자료형을 저장하는 균형잡힌 이진트리 생성
set<int> s;
//원소(5) 삽입
s.insert(5);
//6값을 가지는 원소를 찾음 있다면 해당 원소의 주소값, 없다면 s.end()리턴
if(s.find(6)!=s.end())
printf("존재합니다.\n");
else
printf("없습니다.\n");
//저장된 원소의 수를 리턴
printf("%d\n", s.size());
//모든 원소 삭제
s.clear();
//해당 주소의 원소 삭제
//2번째 원소 삭제
s.erase(++s.begin());
return 0;
}
6. pair
2개의 데이터를 저장할 수 있는 변수이다.
#include <iostream>
#include <utility>
using namespace std;
int main(){
//int, int 자료형을 저장하는 변수 선언
pair<int, int> p;
//(4, 5)를 p에 저장
p=make_pair(4, 5);
//c++11부터 가능
p={4, 5};
return 0;
}
7. map
딕셔너리 자료구조이다. 원소의 삽입과 삭제, 탐색 등의 연산은 O(log n)을 보장한다.
#include <iostream>
#include <map>
using namespace std;
int main(){
//int 자료형을 key로 int 자료형을 데이터로 저장하는 딕셔너리 자료구조 생성
map<int, int> m;
//(4, 5)원소 삽입
m.insert(make_pair(4, 5));
//또는
m[5]=6;
//key와 연관된 원소를 pair<키 자료형, 데이터 자료형> 형태로 리턴함
printf("%d\n", m.find(4)->second);
//key와 연관된 원소의 개수를 리턴함
printf("%d\n", m.count(4));
//저장된 원소의 수를 리턴함
printf("%d\n", m.size());
//해당 주소의 원소 삭제
m.erase(++m.begin());
//모든 원소 삭제
m.clear();
return 0;
}
8. algorithm
자주 사용되는 알고리즘이 들어있는 헤더파일이다.
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
bool cmp(const int a, const int b){
return a>b;
}
int main(){
int arr1[100000];
vector<int> arr2[100000];
int n=100000;
//sort
//첫 원소의 주소와 마지막 원소의 다음 주소를 인자로 넘겨준다.
sort(arr1, arr1+n);
sort(arr2.begin(), arr2.end());
//비교 함수도 만들어서 같이 넘겨줄 수 있다.
sort(arr1, arr1+n, cmp);
//stable_sort
//사용법은 같다.
stable_sort(arr1, arr1+n);
//lower_bound
//첫 원소의 주소와 마지막 원소의 다음 주소와 비교할 원소를 넘겨준다.
//구간내의 원소들은 정렬되어 있어야한다.
//리턴 값은 해당 원소의 주소값이다. 없다면 arr1+n을 리턴한다.
//또는 arr2.end()를 리턴한다.
int idx=lower_bound(arr1, arr1+n, 42)-arr1;
printf("%d\n", idx);
//upper_bound
//사용법은 같다.
vector<int>::iterator it=upper_bound(arr2.begin(), arr2.end(), 54);
if(it!=arr2.end())
printf("%d\n", *it);
//max_element
//첫 원소의 주소와 마지막 원소의 다음 주소를 인자로 넘겨준다.
//구간내의 최대값을 가지는 원소의 주소를 리턴한다.
printf("%d\n", *max_element(arr1, arr1+n));
//min_element
//사용법은 같다.
printf("%d\n", *min_element(arr2.begin(), arr2.end()));
//unique
//첫 원소의 주소와 마지막 원소의 다음 주소를 인자로 넘겨준다.
//구간내의 중복된 원소를 구간의 끝부분으로 밀어주고 마지막 원소의 다음 주소를 리턴한다.
//구간내의 원소들은 정렬되어 있어야한다.
//보통 erase와 함께 중복된 원소를 제거하는 방법으로 사용한다.
arr2.erase(unique(arr2.begin(), arr2.end()), arr2.end());
//next_permutation
//첫 원소의 주소와 마지막 원소의 다음 주소를 인자로 넘겨준다.
//구간내의 원소들의 다음 순열을 생성하고 true를 리턴한다.
//다음 순열이 없다면 false를 리턴한다.
//구간내의 원소들은 정렬되어 있어야한다.
int arr[10];
for(int i=0;i<10;i++)
arr[i]=i;
do{
for(int i=0;i<10;i++)
printf("%d ", arr[i]);
printf("\n");
}while(next_permutaion(arr, arr+10));
return 0;
}
참고자료
- 위키 백과 - 시간 복잡도
- https://baactree.tistory.com/26
- https://baactree.tistory.com/29
- https://blog.chulgil.me/algorithm/